The Measurement class is a utility that provides a
consistent way of handling a diverse range of measurements for bundle
developers. Its purpose is to simplify the correct handling of
measurements in OSGi Frameworks.
OSGi bundle developers from all over the world have different preferences for measurement units, such as feet versus meters. In an OSGi environment, bundles developed in different parts of the world can and will exchange measurements when collaborating.
Distributing a measurement such as a simple floating point number requires the correct and equal understanding of the measurement's semantic by both the sender and the receiver. Numerous accidents have occurred due to misunderstandings between the sender and receiver because there are so many different ways to represent the same value. For example, on September 23, 1999, the Mars Polar Lander was lost because calculations used to program the craft's trajectory were input with English units while the operation documents specified metric units. See [5] Mars Polar Lander failure for more information.
This Measurement and State Specification defines the norm that should be used by all applications that execute in an OSGi Framework. This specification also provides utility classes.
-
Numerical error - All floating point measurements should be able to have a numerical error.
-
Numerical error calculations simplification - Support should be provided to simplify measurements calculations.
-
Unit conflict resolution - It must not be possible to perform addition or subtraction with different units when they are not compatible. For example, it must not be possible to add meters to amperes or watts to pascals.
-
Unit coercion - Multiplication and division operations involving more than one type of measurement must result in a different unit. For example, if meters are divided by seconds, the result must be a new unit that represents
m/s. -
Time-stamp - Measurements should contain a time-stamp so that bundles can determine the age of a particular measurement.
-
Support for floating and discrete values - Both floating point values (64 bit Java
doublefloats) and discrete measurements (32 bit Javaint) should be supported. -
Consistency - The method of error calculation and handling of unit types should be consistent.
-
Presentation - The format of measurements and specified units should be easy to read and understand.
-
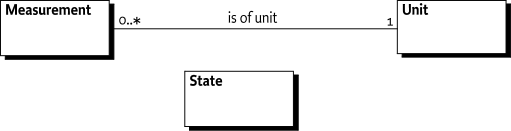
Measurement object - A
Measurementobject contains adoublevalue, adoubleerror, and a long time-stamp. It is associated with aUnitobject that represents its type. -
State object - A State object contains a discrete measurement (
int) with a time-stamp and a name. -
Unit object - A
Unitobject represents a unit such as meter, second, mol, or Pascal. A number ofUnitobjects are predefined and have common names. OtherUnitobjects are created as needed from the 7 basic Système International d'Unité (SI) units. Different units are not used when a conversion is sufficient. For example, the unit of aMeasurementobject for length is always meters. If the length is needed in feet, then the number of feet is calculated by multiplying the value of theMeasurementobject in meters with the necessary conversion factor. -
Error - When a measurement is taken, it is never accurate. This specification defines the error as the value that is added and subtracted to the value to produce an interval, where the probability is 95% that the actual value falls within this interval.
-
Unit - A unit is the type of a measurement: meter, feet, liter, gallon etc.
-
Base Unit - One of the 7 base units defined in the SI.
-
Derived SI unit - A unit is a derived SI unit when it is a combination of exponentiated base units. For example, a volt (
V) is a derived unit because it can be expressed as (m2 ×kg) / (s3 ×A), wherem,kg,sandAare all base units. -
Quantitative derivation - A unit is quantitatively derived when it is converted to one of the base units or derived units using a conversion formula. For example, kilometers (
km) can be converted to meters (m), gallons can be converted to liters, or horsepower can be converted to watts.
A Measurement object contains a value, an error, and a
time-stamp It is linked to a Unit object that describes the
measurement unit in an SI Base Unit or Derived SI Unit.
The value of the Measurement object is the measured
value. It is set in a constructor. The type of the value is
double.
The Measurement object can contain a numerical error.
This error specifies an interval by adding and subtracting the error
value from the measured value. The type of the error is
double. A valid error value indicates that the actual
measured value has a 95% chance of falling within this interval (see
Figure 704.2). If the error is not known it should be
represented as a Double.NaN.
When a Measurement object is created, the time-stamp
can be set. A time-stamp is a long value representing the
number of milliseconds since the epoch midnight of January 1, 1970, UTC
(this is the value from System.currentTimeMillis()
method).
By default, a time-stamp is not set because the call to
System.currentTimeMillis() incurs overhead. If the
time-stamp is not set when the Measurement object is
created, then its default value is zero. If the time-stamp is set, the
creator of the Measurement object must give the time as an
argument to the constructor. For example:
Measurement m = new Measurement(
v, e, null, System.currentTimeMillis() );Once a measurement is taken, it often is used in
calculations. The error value assigned to the result of a calculation
depends largely on the error values of the operands. Therefore, the
Measurement class offers addition, subtraction,
multiplication, and division functions for measurements and constants.
These functions take the error into account when performing the specific
operation.
The Measurement class uses absolute errors and has
methods to calculate a new absolute error when multiplication, division,
addition, or subtraction is performed. Error calculations must therefore
adhere to the rules listed in the following table. In this table, Δa is the absolute positive
error in a value a and Δ b is the absolute positive
error in a value b. c is a
constant floating point value without an error.
Table 704.1 Error Calculation Rules
| Calculation | Function | Error |
|---|---|---|
|
a × b |
mul(Measurement) |
| Δa × b | + | a × Δb | |
|
a / b |
div(Measurement) |
( | Δa × b | + | a × Δb | ) / b2 |
|
a + b |
add(Measurement) |
Δa + Δb |
|
a - b |
sub(Measurement) |
Δa + Δb |
|
a × c |
mul(double) |
| Δa × c | |
|
a / c |
div(double) |
| Δa / c | |
|
a + c |
add(double) |
Δa |
|
a - c |
sub(double) |
Δa |
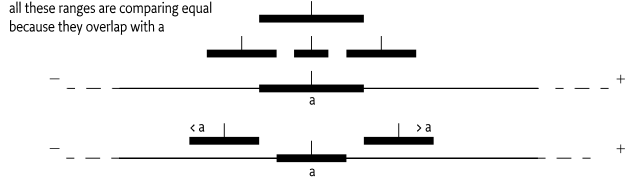
Measurement objects have a value and an error range, making comparing and constructing these objects more complicated than normal scalars.
The Measurements object has the following constructors that the value, error, unit and timestamp:
Both equals(Object) and hashCode() methods are overridden to provide value-based equality. Two Measurement objects are equal when the unit, error, and value are the same. The time-stamp is not relevant for equality or the hash code.
The Measurement class implements the
java.lang.Comparable interface and thus implements the
compareTo(Object) method. Comparing two Measurement
objects is not straightforward, however, due to the associated error.
The error effectively creates a range, so comparing two
Measurement objects is actually comparing intervals.
Two Measurement objects are
considered to be equal when their intervals overlap. In all other cases,
the value is used in the comparison.
This comparison implies that the equals(Object) method may return false while the
compareTo(Object) method returns 0 for the same
Measurement object.
Each Measurement object is related to a
Unit object. The Unit object defines the unit of
the measurement value and error. For example, the Unit object might define
the unit of the measurement value and the error as meters
(m). For convenience, the Unit class defines a
number of standard units as constants. Measurement objects
are given a specific Unit with the constructor. The following
example shows how a measurement can be associated with meters
(m):
Measurement length = new Measurement( v, 0.01,Unit.m );Units are based on the Système International d'Unité (SI), developed after the French Revolution. The SI consists of 7 different units that can be combined in many ways to form a large series of derived units. The basic 7 units are listed in the following table. For more information, see [2] General SI index.
Additional units are derived in the following ways:
Derived units can be a combination of exponentiated base units. For
example, Hz (Hertz) is the unit for frequencies and is
actually derived from the calculation of 1/s. A more
complicated derived unit is volt (V). A volt is
actually:
( m2 × kg ) / ( s3 × A )The SI defines various derived units with their own name, for
example pascal (Pa), watt (W), volt
(V), and many more.
The Measurement class must maintain its unit by keeping
track of the exponents of the 7 basic SI units.
If different units are used in addition or subtraction of
Measurement objects, an ArithmeticException must
be thrown.
Measurement length = new Measurement( v1,0.01, Unit.m );
Measurement duration = new Measurement( v2, 0, Unit.s );
try {
Measurement r = length.add( duration );
}
catch( ArithmeticException e ) {
// This must be thrown
}When two Measurement objects are
multiplied, the Unit object of the result contains the sum of
the exponents. When two Measurement objects are divided, the
exponents of the Unit object of the result are calculated by
subtraction of the exponents.
The Measurement class must support exponents of -64 to
+63. Overflow must not be reported but must result in an invalid
Unit object. All calculations with an invalid
Unit object should result in an invalid Unit
object. Typical computations generate exponents for units between +/-
4.
The base and derived units can be converted to other units that are of the same quality, but require a conversion because their scales and offsets may differ. For example, degrees Fahrenheit, kelvin, and Celsius are all temperatures and, therefore, only differ in their quantity. Kelvin and Celsius are the same scale and differ only in their starting points. Fahrenheit differs from kelvin in that both scale and starting point differ.
Using different Unit objects for the units that
differ only in quantity can easily introduce serious software bugs.
Therefore, the Unit class utilizes the SI units. Any
exchange of measurements should be done using SI units to prevent these
errors. When a measurement needs to be displayed, the presentation logic
should perform the necessary conversions to present it in a localized
form. For example, when speed is presented in a car purchased in the
United States, it should be presented as miles instead of meters.
The adoption of the SI in the United States and the United Kingdom has met with resistance. This issue raises the question why the SI system has to be the preferred measurement system in the OSGi Specifications.
The SI system is utilized because it is the only
measurement system that has a consistent set of
base units. The base units can be combined to create a large number of
derived units without requiring a large number of complicated conversion
formulas. For example, a watt is simply a combination of meters,
kilograms, and seconds (
m2×kg /
s3). In contrast, horsepower is
not easily related to inches, feet, fathoms, yards, furlongs, ounces,
pounds, stones, or miles. This difficulty is the reason that science has
utilized the SI for a long time. It is also the reason that the SI has
been chosen as the system used for the Measurement
class.
The purpose of the Measurement class is internal,
however, and should not restrict the usability of the OSGi environment.
Users should be able to use the local measurement units when data is
input or displayed. This choice is the responsibility of the application
developer.
The State object is used to represent discrete states.
It contains a time-stamp but does not contain an error or
Unit object. The Measurement object is not
suitable to maintain discrete states. For example, a car door can be
LOCKED, UNLOCKED, or CHILDLOCKED.
Measuring and operating with these values does not require error
calculations, nor does it require SI units. Therefore, the
State object is a simple, named object that holds an integer
value.
The open source project Kawa, a scheme-based Java environment, has
included a gnu.math library that contains unit handling
similar to this specification. It can be found at [4] A Math Library containing unit handling in Kawa.
The library seems considerably more complex without offering much more functionality than this specification. It also does not strictly separate basic SI units such as meter from quantitatively derived units such as pica.
The Measurement, Unit and
State classes have been made immutable. Instances of these
classes can be freely handed out to other bundles because they cannot be
extended, nor can the value, error, or time-stamp be altered after the
object is created.
Measurement Package Version 1.0.
Bundles wishing to use this package must list the package in the Import-Package header of the bundle's manifest.
Example import for consumers using the API in this package:
Import-Package: org.osgi.util.measurement; version="[1.0,2.0)"
-
Measurement- Represents a value with an error, a unit and a time-stamp. -
State- Groups a state name, value and timestamp. -
Unit- A unit system for measurements.
Represents a value with an error, a unit and a time-stamp.
A Measurement object is used for maintaining the tuple of value,
error, unit and time-stamp. The value and error are represented as doubles
and the time is measured in milliseconds since midnight, January 1, 1970 UTC.
Mathematic methods are provided that correctly calculate taking the error into account. A runtime error will occur when two measurements are used in an incompatible way. E.g., when a speed (m/s) is added to a distance (m). The measurement class will correctly track changes in unit during multiplication and division, always coercing the result to the most simple form. See Unit for more information on the supported units.
Errors in the measurement class are absolute errors. Measurement errors should use the P95 rule. Actual values must fall in the range value +/- error 95% or more of the time.
A Measurement object is immutable in order to be easily shared.
Note: This class has a natural ordering that is inconsistent with equals. See compareTo(Object).
Immutable
The value of the Measurement.
The error of the Measurement.
The Unit object in which the value is measured. If
this argument is null, then the unit will be set to
Unit.unity.
The time measured in milliseconds since midnight, January 1, 1970 UTC.
Create a new Measurement object.
The value of the Measurement.
The error of the Measurement.
The Unit object in which the value is measured. If
this argument is null, then the unit will be set to
Unit.unity.
Create a new Measurement object with a time of zero.
The value of the Measurement.
The Unit in which the value is measured. If this
argument is null, then the unit will be set to
Unit.unity.
Create a new Measurement object with an error of 0.0 and a time
of zero.
The value of the Measurement.
Create a new Measurement object with an error of 0.0, a unit of
Unit.unity and a time of zero.
The Measurement object that will be added with this
object.
Returns a new Measurement object that is the sum of this object
added to the specified object.
The error and unit of the new object are computed. The time of the new
object is set to the time of this object.
A new Measurement object that is the sum of this and m.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be added.
The value that will be added with this object.
The Unit object of the specified value.
Returns a new Measurement object that is the sum of this object
added to the specified value.
A new Measurement object that is the sum of this object
added to the specified value. The unit of the new object is
computed. The error and time of the new object is set to the
error and time of this object.
ArithmeticException– If the Unit objects of this object
and the specified value cannot be added.
The value that will be added with this object.
Returns a new Measurement object that is the sum of this object
added to the specified value.
A new Measurement object that is the sum of this object
added to the specified value. The error, unit, and time of the
new object is set to the error, Unit and time of this
object.
The object to be compared.
Compares this object with the specified object for order. Returns a negative integer, zero, or a positive integer if this object is less than, equal to, or greater than the specified object.
Note: This class has a natural ordering that is inconsistent with equals.
For this method, another Measurement object is considered equal
if there is some x such that
getValue() - getError() <= x <= getValue() + getError()
for both Measurement objects being compared.
A negative integer, zero, or a positive integer if this object is less than, equal to, or greater than the specified object.
ClassCastException– If the specified object is not of type
Measurement.
ArithmeticException– If the unit of the specified
Measurement object is not equal to the Unit
object of this object.
The Measurement object that will be the divisor of this
object.
Returns a new Measurement object that is the quotient of this
object divided by the specified object.
A new Measurement object that is the quotient of this
object divided by the specified object. The error and unit of the
new object are computed. The time of the new object is set to the
time of this object.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be divided.
The value that will be the divisor of this object.
The Unit object of the specified value.
Returns a new Measurement object that is the quotient of this
object divided by the specified value.
A new Measurement that is the quotient of this object
divided by the specified value. The error and unit of the new
object are computed. The time of the new object is set to the
time of this object.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be divided.
The value that will be the divisor of this object.
Returns a new Measurement object that is the quotient of this
object divided by the specified value.
A new Measurement object that is the quotient of this
object divided by the specified value. The error of the new
object is computed. The unit and time of the new object is set to
the Unit and time of this object.
The object to compare with this object.
Returns whether the specified object is equal to this object. Two
Measurement objects are equal if they have same value, error and
Unit.
Note: This class has a natural ordering that is inconsistent with equals. See compareTo(Object).
true if this object is equal to the specified object;
false otherwise.
Returns the error of this Measurement object. The error is always
a positive value.
The error of this Measurement as a double.
Returns the time at which this Measurement object was taken. The
time is measured in milliseconds since midnight, January 1, 1970 UTC, or
zero when not defined.
The time at which this Measurement object was taken or
zero.
Returns the Unit object of this Measurement object.
The Unit object of this Measurement object.
Returns the value of this Measurement object.
The value of this Measurement object as a double.
Returns a hash code value for this object.
A hash code value for this object.
The Measurement object that will be multiplied with this
object.
Returns a new Measurement object that is the product of this
object multiplied by the specified object.
A new Measurement that is the product of this object
multiplied by the specified object. The error and unit of the new
object are computed. The time of the new object is set to the
time of this object.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be multiplied.
The value that will be multiplied with this object.
The Unit of the specified value.
Returns a new Measurement object that is the product of this
object multiplied by the specified value.
A new Measurement object that is the product of this
object multiplied by the specified value. The error and unit of
the new object are computed. The time of the new object is set to
the time of this object.
ArithmeticException– If the units of this object and the specified
value cannot be multiplied.
The value that will be multiplied with this object.
Returns a new Measurement object that is the product of this
object multiplied by the specified value.
A new Measurement object that is the product of this
object multiplied by the specified value. The error of the new
object is computed. The unit and time of the new object is set to
the unit and time of this object.
The Measurement object that will be subtracted from this
object.
Returns a new Measurement object that is the subtraction of the
specified object from this object.
A new Measurement object that is the subtraction of the
specified object from this object. The error and unit of the new
object are computed. The time of the new object is set to the
time of this object.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be subtracted.
The value that will be subtracted from this object.
The Unit object of the specified value.
Returns a new Measurement object that is the subtraction of the
specified value from this object.
A new Measurement object that is the subtraction of the
specified value from this object. The unit of the new object is
computed. The error and time of the new object is set to the
error and time of this object.
ArithmeticException– If the Unit objects of this object
and the specified object cannot be subtracted.
The value that will be subtracted from this object.
Returns a new Measurement object that is the subtraction of the
specified value from this object.
A new Measurement object that is the subtraction of the
specified value from this object. The error, unit and time of the
new object is set to the error, Unit object and time of
this object.
Groups a state name, value and timestamp.
The state itself is represented as an integer and the time is measured in milliseconds since midnight, January 1, 1970 UTC.
A State object is immutable so that it may be easily shared.
Immutable
The value of the state.
The name of the state.
The time measured in milliseconds since midnight, January 1, 1970 UTC.
Create a new State object.
The value of the state.
The name of the state.
Create a new State object with a time of 0.
The object to compare with this object.
Return whether the specified object is equal to this object. Two
State objects are equal if they have same value and name.
true if this object is equal to the specified object;
false otherwise.
Returns the name of this State.
The name of this State object.
Returns the time with which this State was created.
The time with which this State was created. The time is
measured in milliseconds since midnight, January 1, 1970 UTC.
Returns the value of this State.
The value of this State object.
Returns a hash code value for this object.
A hash code value for this object.
A unit system for measurements. This class contains definitions of the most common SI units.
This class only support exponents for the base SI units in the range -64 to
+63. Any operation which produces an exponent outside of this range will
result in a Unit object with undefined exponents.
Immutable
The electric charge unit coulomb (C).
coulomb is expressed in SI units as s·A
The capacitance unit farad (F).
farad is equal to C/V or is expressed in SI units as s4·A2/m2·kg
The absorbed dose unit gray (Gy).
Gy is equal to J/kg or is expressed in SI units as m2/s2
The frequency unit hertz (Hz).
hertz is expressed in SI units as 1/s
The energy unit joule (J).
joule is equal to N·m or is expressed in SI units as m2·kg/s2
The catalytic activity unit katal (kat).
katal is expressed in SI units as mol/s
The illuminance unit lux (lx).
lux is expressed in SI units as cd/m2
The force unit newton (N).
N is expressed in SI units as m·kg/s2
The electric resistance unit ohm.
ohm is equal to V/A or is expressed in SI units as m2·kg/s3·A2
The pressure unit pascal (Pa).
Pa is equal to N/m2 or is expressed in SI units as kg/m·s2
The electric conductance unit siemens (S).
siemens is equal to A/V or is expressed in SI units as s3·A2/m2·kg
The magnetic flux density unit tesla (T).
tesla is equal to Wb/m2 or is expressed in SI units as kg/s2·A
The electric potential difference unit volt (V).
volt is equal to W/A or is expressed in SI units as m2·kg/s3·A
The power unit watt (W).
watt is equal to J/s or is expressed in SI units as m2·kg/s3
The magnetic flux unit weber (Wb).
weber is equal to V·s or is expressed in SI units as m2·kg/s2·A
the Unit object that should be checked for equality
Checks whether this Unit object is equal to the specified
Unit object. The Unit objects are considered equal if
their exponents are equal.
true if the specified Unit object is equal to this
Unit object.
[1]SI Units informationhttp://physics.nist.gov/cuu/Units
[2]General SI indexhttp://en.wikipedia.org/wiki/SI
[3]JSR 108 Units Specificationhttp://www.jcp.org/jsr/detail/108.jsp
[4]A Math Library containing unit handling in Kawahttp://www.gnu.org/software/kawa
[5]Mars Polar Lander failurehttp://mars.jpl.nasa.gov/msp98/news/mco990930.html